Table of Contents
IntroductionApplication: Connected ComponentsApplication: Graph Two-ColoringDFSBFSPrerequisite - Queues & DequesQueuesDequesImplementationSolution - Building RoadsDFS SolutionAn Issue With Deep RecursionBFS SolutionConnected Component ProblemsSolution - Building TeamsDFS SolutionBFS SolutionGraph Two-Coloring ProblemsGraph Traversal
Authors: Siyong Huang, Benjamin Qi, Ryan Chou
Contributors: Andrew Wang, Jason Chen, Divyanshu Upreti
Traversing a graph with depth first search and breadth first search.
Table of Contents
IntroductionApplication: Connected ComponentsApplication: Graph Two-ColoringDFSBFSPrerequisite - Queues & DequesQueuesDequesImplementationSolution - Building RoadsDFS SolutionAn Issue With Deep RecursionBFS SolutionConnected Component ProblemsSolution - Building TeamsDFS SolutionBFS SolutionGraph Two-Coloring ProblemsIntroduction
| Resources | ||||
|---|---|---|---|---|
| CPH | ||||
The purpose of graph traversal algorithms is to visit all nodes within a graph in a certain order and compute some information along the way. Two common algorithms for doing this are depth first search (DFS) and breadth first search (BFS).
Application: Connected Components
Focus Problem – try your best to solve this problem before continuing!
A connected component is a maximal set of connected nodes in an undirected graph. In other words, two nodes are in the same connected component if and only if they can reach each other via edges in the graph.
In the above focus problem, the goal is to add the minimum possible number of edges such that the entire graph forms a single connected component.
Application: Graph Two-Coloring
Focus Problem – try your best to solve this problem before continuing!
Graph two-coloring refers to assigning a boolean value to each node of the graph, dictated by the edge configuration. The most common example of a two-colored graph is a bipartite graph, in which each edge connects two nodes of opposite colors.
In the above focus problem, the goal is to assign each node (friend) of the graph to one of two colors (teams), subject to the constraint that edges (friendships) connect two nodes of opposite colors. In other words, we need to check whether the input is a bipartite graph and output a valid coloring if it is.
DFS
| Resources | ||||
|---|---|---|---|---|
| CSA | up to but not including "More about DFS" | |||
| CPH | example diagram + code | |||
From the second resource:
Depth-first search (DFS) is a straightforward graph traversal technique. The algorithm begins at a starting node, and proceeds to all other nodes that are reachable from the starting node using the edges of the graph.
Depth-first search always follows a single path in the graph as long as it finds new nodes. After this, it returns to previous nodes and begins to explore other parts of the graph. The algorithm keeps track of visited nodes, so that it processes each node only once.
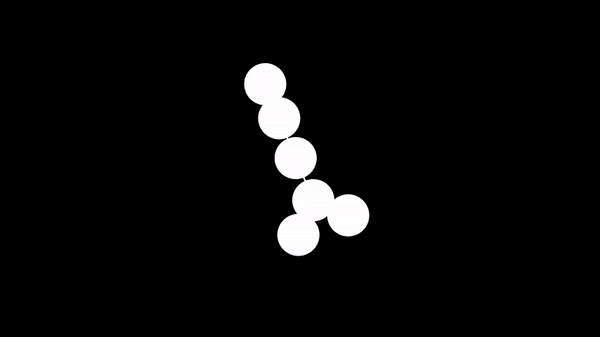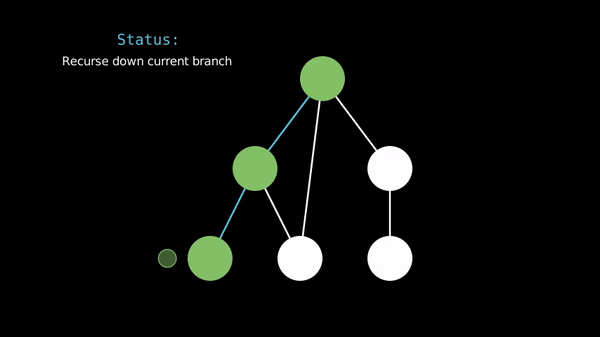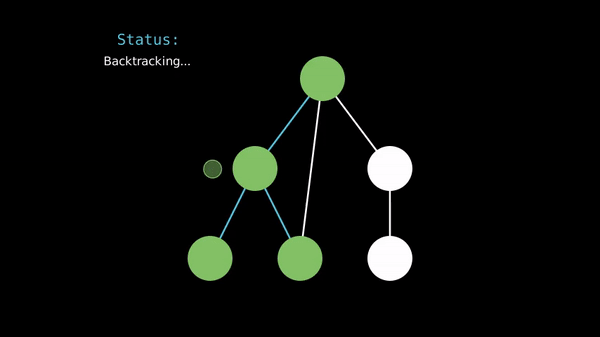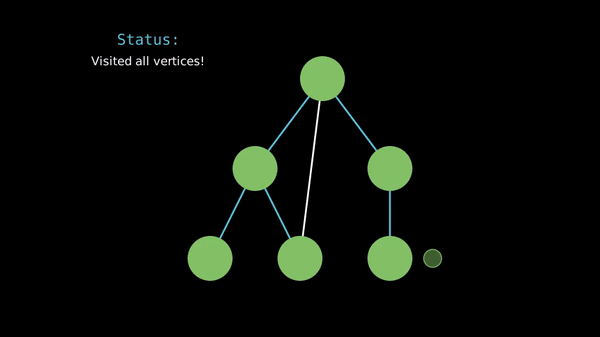
When implementing DFS, we often use a recursive function to visit the vertices and an array to store whether we've seen a vertex before.
C++
#include <bits/stdc++.h>using namespace std;int n = 6;vector<vector<int>> adj(n);vector<bool> visited(n);void dfs(int current_node) {if (visited[current_node]) { return; }visited[current_node] = true;
Java
import java.io.*;import java.util.*;public class DFSDemo {static List<Integer>[] adj;static boolean[] visited;static int n = 6;public static void main(String[] args) throws IOException {visited = new boolean[n];
Python
import syssys.setrecursionlimit(10**5) # Python has a default recursion limit of 1000n = 6visited = [False] * n"""Define adjacency list and read in problem-specific input here.
BFS
| Resources | ||||
|---|---|---|---|---|
| CSA | interactive, implementation | |||
| PAPS | grid, 8-puzzle examples | |||
| cp-algo | common applications | |||
| KA | ||||
| YouTube | If you prefer a video format | |||
In a breadth-first search, we travel through the vertices in order of their distance from the starting vertex.
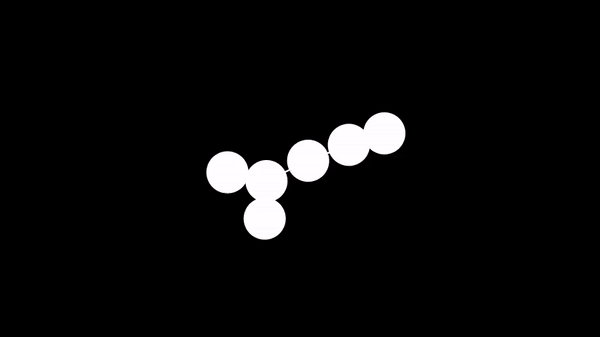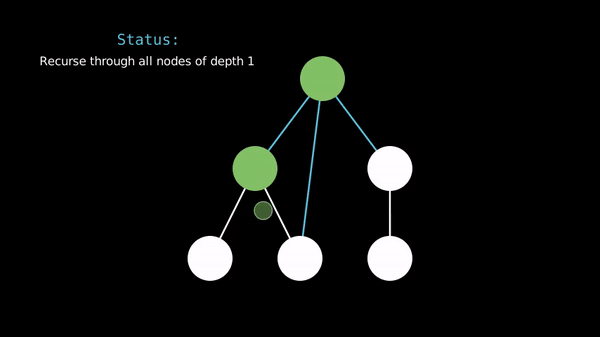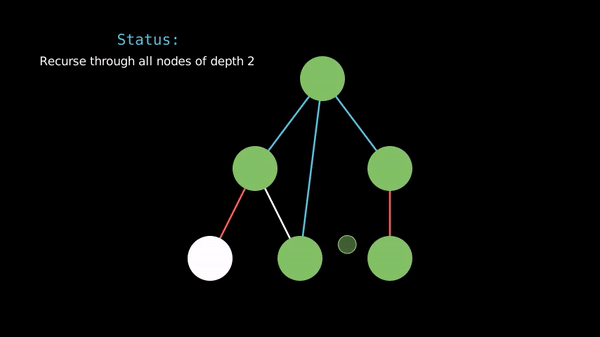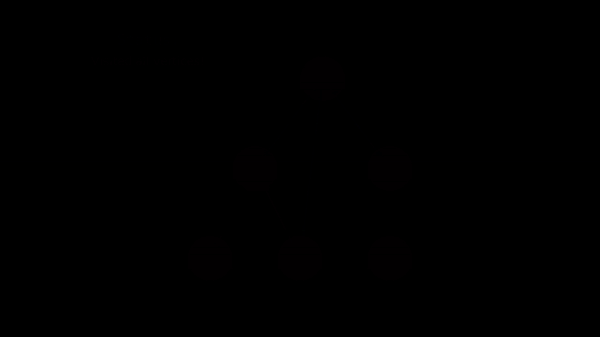
Prerequisite - Queues & Deques
| Resources | ||||
|---|---|---|---|---|
| CPH | ||||
| PAPS | ||||
Queues
A queue is a First In First Out (FIFO) data structure that supports three operations, all in time.
C++
push: inserts at the back of the queuepop: deletes from the front of the queuefront: retrieves the element at the front without removing it.
queue<int> q;q.push(1); // [1]q.push(3); // [3, 1]q.push(4); // [4, 3, 1]q.pop(); // [4, 3]cout << q.front() << endl; // 3
Java
add: insertion at the back of the queuepoll: deletion from the front of the queuepeek: which retrieves the element at the front without removing it
Java doesn't actually have a Queue class; it's only an interface. The most
commonly used implementation is the LinkedList, declared as follows:
Queue<Integer> q = new LinkedList<Integer>();q.add(1); // [1]q.add(3); // [3, 1]q.add(4); // [4, 3, 1]q.poll(); // [4, 3]System.out.println(q.peek()); // 3
Python
Python has a queue built-in module.
Queue.put(n): Inserts element to the back of the queue.Queue.get(): Gets and removes the front element. If the queue is empty, this will wait forever, creating a TLE error.Queue.queue[n]: Gets the nth element without removing it. Set n to 0 for the first element.
from queue import Queueq = Queue() # []q.put(1) # [1]q.put(2) # [1, 2]v = q.queue[0] # v = 1, q = [1, 2]v = q.get() # v = 1, q = [2]v = q.get() # v = 2, q = []v = q.get() # Code waits forever, creating TLE error.
Warning!
Python's queue.Queue() uses Locks to maintain a threadsafe synchronization, so it's quite slow.
To avoid TLE, use collections.deque() instead for a faster version of a queue.
Deques
A deque (usually pronounced "deck") stands for double ended queue and is a combination of a stack and a queue, in that it supports insertions and deletions from both the front and the back of the deque. Not very common in Bronze / Silver.
C++
The four methods for adding and removing are push_back, pop_back,
push_front, and pop_front.
deque<int> d;d.push_front(3); // [3]d.push_front(4); // [4, 3]d.push_back(7); // [4, 3, 7]d.pop_front(); // [3, 7]d.push_front(1); // [1, 3, 7]d.pop_back(); // [1, 3]
You can also access deques in constant time like an array in constant time with
the [] operator. For example, to access the th element of a
deque , do .
Java
In Java, the deque class is called ArrayDeque. The four methods for adding and
removing are addFirst , removeFirst, addLast, and removeLast.
ArrayDeque<Integer> deque = new ArrayDeque<Integer>();deque.addFirst(3); // [3]deque.addFirst(4); // [4, 3]deque.addLast(7); // [4, 3, 7]deque.removeFirst(); // [3, 7]deque.addFirst(1); // [1, 3, 7]deque.removeLast(); // [1, 3]
Python
In Python, collections.deque() is used for a deque data structure. The four methods for adding and removing are appendleft, popleft, append, and pop.
d = collections.deque()d.appendleft(3) # [3]d.appendleft(4) # [4, 3]d.append(7) # [4, 3, 7]d.popleft() # [3, 7]d.appendleft(1) # [1, 3, 7]d.pop() # [1, 3]
Implementation
When implementing BFS, we often use a queue to track the next vertex to visit. Like DFS, we'll also keep an array to store whether we've seen a vertex before.
Java
static final int MAX_N = (int)1e6;public static void main(String[] args) throws IOException {boolean[] visited = new boolean[MAX_N];ArrayList<ArrayList<Integer>> adj = new ArrayList<ArrayList<Integer>>();for (int i = 0; i < MAX_N; i++) adj.add(new ArrayList<Integer>());/** Define adjacency list and read in problem-specific input*
C++
int n = 6;vector<vector<int>> adj(n);vector<bool> visited(n);int main() {/** Define adjacency list and read in problem-specific input** In this example, we've provided "dummy input" that's* reflected in the GIF above to help illustrate the
Python
from collections import deque"""Define adjacency list and read in problem-specific inputIn this example, we've provided "dummy input" that'sreflected in the GIF above to help illustrate theorder of the recrusive calls."""
Solution - Building Roads
Note that each edge decreases the number of connected components by either zero or one. So you must add at least edges, where is the number of connected components in the input graph.
To compute , iterate through each node. If it has not been visited, visit it and all other nodes in its connected component using DFS or BFS. Then equals the number of times we perform the visiting operation.
There are many valid ways to pick new roads to build. One way is to choose a single representative from each of the components and link them together in a line.
DFS Solution
C++
#include <iostream>#include <vector>using namespace std;int N;vector<vector<int>> adj;vector<bool> visited;vector<int> rep;
Java
import java.io.*;import java.util.*;public class Main {public static ArrayList<Integer> adj[];public static ArrayList<Integer> rep = new ArrayList<Integer>();public static boolean visited[];public static void main(String[] args) throws IOException {BufferedReader br =new BufferedReader(new InputStreamReader(System.in));
Python
def solve(n, adj):unvisited = set(range(1, n + 1))starts = set()def dfs(current):for next in adj[current]:if next in unvisited:unvisited.remove(next)dfs(next)
However, this code causes a runtime error on five test cases. See the next subsection for how to fix this.
An Issue With Deep Recursion
C++
If you run the solution code locally on the line graph generated by the following code:
N = 100000print(N, N - 1)for i in range(1, N):print(i, i + 1)
then you might get a segmentation fault even though your code passes on the
online judge. This occurs because every recursive call contributes to the size
of the call stack, which
is limited to a few megabytes by default. To increase the stack size, refer to
this module.
Short answer: If you would normally compile your code with g++ sol.cpp,
then compile it with g++ -Wl,-stack_size,0xF0000000 sol.cpp instead.
Java
If you run the solution code locally on the line graph generated by the following code:
N = 100000print(N, N - 1)for i in range(1, N):print(i, i + 1)
then you might get a StackOverflowError even though your code passes on the
online judge. This occurs because every recursive call contributes to the size
of the call stack, which is limited
to less than a megabyte by default. To resolve this, you can pass an
option of the form -Xss... to run the code with an increased stack size.
For example, java -Xss512m Main will run the code with a stack size limit of 512 megabytes.
Python
If you run the solution code on the line graph generated by the following code:
N = 100000print(N, N - 1)for i in range(1, N):print(i, i + 1)
then you will observe a RecursionError that looks like this:
Traceback (most recent call last): File "input/code.py", line 28, in <module> solve(n, adj) File "input/code.py", line 14, in solve dfs(start, start) File "input/code.py", line 9, in dfs dfs(start, next) File "input/code.py", line 9, in dfs dfs(start, next) File "input/code.py", line 9, in dfs dfs(start, next) [Previous line repeated 994 more times] File "input/code.py", line 7, in dfs if next in unvisited: RecursionError: maximum recursion depth exceeded in comparison
This will occur for since the recursion limit in Python is set to 1000 by default. We can fix this by increasing the recursion limit:
import syssys.setrecursionlimit(1000000)Code Snippet: rest of solution (Click to expand)
although we still get TLE on two test cases. To resolve this, we can implement a BFS solution, as shown below.
BFS Solution
C++
#include <bits/stdc++.h>using namespace std;int main() {int n, m;cin >> n >> m;vector<vector<int>> adj(n);for (int i = 0; i < m; i++) {int u, v;
Python
from collections import dequen, m = map(int, input().split())adj = [[] for _ in range(n)]for _ in range(m):u, v = map(int, input().split())adj[u - 1].append(v - 1)adj[v - 1].append(u - 1)
Connected Component Problems
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| Silver | Easy | Show TagsConnected Components | |||
| Silver | Easy | ||||
| Silver | Easy | Show TagsConnected Components | |||
| Kattis | Easy | Show TagsConnected Components | |||
| DMOJ | Easy | Show TagsDFS | |||
| CSES | Normal | ||||
| Gold | Normal | Show TagsBinary Search, Connected Components | |||
| Silver | Normal | Show TagsBinary Search, Connected Components | |||
| Silver | Normal | Show Tags2P, Binary Search, Connected Components | |||
| Silver | Normal | Show TagsDFS | |||
| CF | Hard | Show TagsDFS, Sorted Set | |||
| Kattis | Very Hard | Show TagsBinary Search, Connected Components | |||
| Silver | Very Hard | Show TagsConstructive, Cycles, Spanning Tree |
Solution - Building Teams
| Resources | ||||
|---|---|---|---|---|
| CPH | Brief solution sketch with diagrams. | |||
| IUSACO | ||||
| cp-algo | ||||
| CP2 | ||||
The idea is that for each connected component, we can arbitrarily label a node and then run DFS or BFS. Every time we visit a new (unvisited) node, we set its color based on the edge rule. When we visit a previously visited node, check to see whether its color matches the edge rule.
DFS Solution
Optional: Adjacency List Without an Array of Vectors
See here.
C++
#include <cstdio>#include <vector>const int MN = 1e5 + 10;int N, M;bool bad, vis[MN], group[MN];std::vector<int> a[MN];void dfs(int n = 1, bool g = 0) {
Java
Warning!
Because Java is so slow, an adjacency list using lists/arraylists results in TLE. Instead, the Java sample code uses the edge representation mentioned in the optional block above.
import java.io.*;import java.util.*;public class BuildingTeams {static InputReader in = new InputReader(System.in);static PrintWriter out = new PrintWriter(System.out);public static final int MN = 100010;public static final int MM = 200010;
BFS Solution
C++
#include <bits/stdc++.h>using namespace std;int main() {cin.tie(0)->sync_with_stdio(0);int n, m;cin >> n >> m;vector<vector<int>> adj(n);
Python
from collections import dequen, m = map(int, input().split())adj = [[] for i in range(n)]for _ in range(m):u, v = map(int, input().split())adj[u - 1].append(v - 1)adj[v - 1].append(u - 1)
Graph Two-Coloring Problems
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| CF | Easy | Show TagsBipartite | |||
| Silver | Easy | Show TagsBipartite | |||
| CF | Easy | Show TagsBipartite | |||
| Baltic OI | Hard | Show TagsDFS, Median | |||
| CC | Hard | Show TagsBipartite, DFS | |||
| APIO | Very Hard | Show TagsBipartite |
Module Progress:
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!